Flow through Pipes
Flow through pipes is mostly associated with Head loss, which makes it important to know several factors that contribute to it.
Basic Concepts one must know to determine head loss in pipes,
Type of flow
Ideal fluid flow: A flow is Ideal if the viscosity is zero. Hence these fluids do not have head loss.
Ex: Air, gases are mostly ideal.
Equations for Ideal flow: Bernoulli Equation, Continuity Equation.
Real fluid flow: The fluids that have viscosity are real.
These fluids have: Friction among their layers, head loss, shear stress
Note: From the definition of Newtonian Fluids
Even if µ=0, τ≠0.
τ =0 only if du/dy =0 i.e. when the fluid is hydrostatic ==at rest.
Conduits:
Open Conduit: In open conduits, the flow is open to atmosphere.
Pressure ≠f(x)
Where x= distance
Closed Conduit: In closed conduits, pressure varies with the pump used and friction.
Pressure=f(x) if the pipe is full.
Pressure ≠f(x) if the pipe is not full.
Circular and Non Circular pipes:
Circular pipes: Most of the water carrying pipes.
Non Circular pipes: Air ducts are generally rectangular.
The flow is also categorized based on the Reynolds No.
If the Reynolds No <2000,>Laminar.
If the Reynolds No>4000, the flow is Turbulent.
If 2000
Major Losses:
Friction between layers of the fluid, friction between fluid and conduit surface causes major losses in a pipe.
Minor losses:
Entry and exit losses: When a fluid enters and exits a pipe, it creates some losses.
Fitting losses: The fittings attached to change the direction of the flow in a pipe, regulates the flow.
This might simultaneously lead to some losses, called fitting losses.
Velocity Distribution under various flow conditions:
Figure 1.Velocity distribution for Laminar and Turbulent flows
Laminar Flow:
The velocity distribution in laminar flow conditions along the cross-section of the pipe will be parabolic (Figure 1) due to the following reasons:
· The friction between layers of the fluid and the wall of the pipe. The fluid being in motion and the pipe being at rest, the velocity at junction of fluid and wall will be equal to zero.
· Also the friction between the layers of the fluid also causes a change in the velocity distribution.
Turbulent Flow:
The velocity distribution turbulent flow conditions along the cross-section of the pipe do not vary much (Figure 1) except for the junctions of the conduit wall with fluid due to the following reasons:
· The particles in the turbulent flow regime are very well mixed, so the velocity remains the almost uniform towards the centre of the pipe.
· Due to the friction between the pipe conduit and fluid layers, the velocity at the interface of conduit and the fluid is almost==0.
Pressure drop derivation for Laminar flow conditions:
Consider a pipe cross-section in which laminar flow conditions exist. Let us take a small element of fluid (Figure 2).
Applying Newton’s second law of motion to the laminar fluid flow,
Under stead flow conditions,
Net force=ΣF=m x a =m (dv/dt)=0
Where p1= pressure force acting on section 1-1
p2= pressure force acting on section 2-2
A=area of the section
τ=Shear stress on the element
Under steady state conditions, ΣF=0
Integrating and substituting the limits, we get
But in case of laminar flow, u avg=umax/2
Therefore pressure drop per unit length,
To calculate the loss due to friction a dimensionless factor f called Darcy’s friction factor defined as
for laminar, viscous flow.
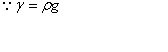
References:
1. Inspired by class (CE 331) of Dr. Nirmala Khandan
Click the above link to access the notes.
Problems will be uploaded soon....
Posts
No comments:
Post a Comment